Searching for a magic square of (mostly) squares
Magic squares have a long history, dating back to at least 2000 BCE in China. Multimagie.com is the authoritative source for the latest status on everything related to magic squares and all their many variants.
One interesting unsolved problem is whether it is possible to construct a 3x3 magic square where all the numbers are perfect squares. The closest known example has 7 squares:
| 3732 | 2892 | 5652 |
| 360721 | 4252 | 232 |
| 2052 | 5272 | 222121 |
Martin Gardner offered a prize of $100 for a magic square of squares in 1996, and now Christan Boyer of multimagie offers a prize of 1000 euros and a bottle of Champagne for any 3x3 magic square which uses 7 or more squares, and is different than the one above (and not just multiplying all its cells by some k2).
The work reported here was mostly done more than 10 years ago, around 2008.
A little background
I found this page useful for some basic background algebra on magic squares, in particular the observation that any 3x3 magic square can be descibed by just the center cell E and two parameters m and n:
| E+n | E-n-m | E+m |
| E-n-m | E | E+n-m |
| E-m | E+n+m | E-n |
The magic sum for any 3x3 square will always be 3E – three times the center cell. This also shows that the four sums which include the center cell – the central row and column and the two diagonals – are arithmetic progressions. This is really useful, because a lot can be said about arithmetic progressions of squares.
A paper by Christian Boyer gives some more useful pointers, and enumerates all of the possible selections of 7 cells from a 3x3 square (with symmetries removed). I’ll reproduce his figure here since it will be useful in the discussion below:
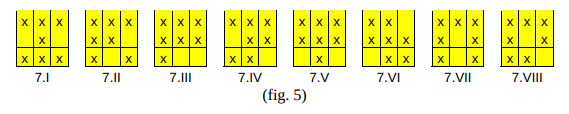
Since the center cell is E and the magic sum is 3E, any two cells symmetric around the center sum to 2E. If those cells are both squares, then 2E is a sum of squares. All of the 7.x configurations shown above require 2E to be a sum of squares in at least 2 different ways.
Sums of squares
A theorem from Fermat tells us that every prime of the form 4k+1 is a sum of two squares, and a number is the sum of two squares if and only if all prime factors of the form 4k+3 have an even exponent in its prime factorization. In other words, only numbers with only factors of the form 4k+1 are of interest to us as possible values for E (the center cell). Any 4k+3 factors would have to be squared, which would end up just multiplying all the cells by that value, which is redundant.
This online calculator from WIMS can decompose a number into sums of two squares in all possible ways, and kindly includes a link to the PARI-based source code, which I incorporated into my program.
Counting decompositions
Jacobi’s two-square theorem says that the number of ways a positive integer can be written as the sum of two squares is four times the difference in the number of divisors congruent to 1 and 3 mod 4. Since all of our factors are of the form 4k+1, it is just four times the number of divisors.
It took a little work for me to understand that Jacobi’s tally includes negative squares and swapping the order of the squares being added. Removing decompositions where one or the other or both squares are negative divides the total by four, and removing one of the orderings of each pair divides it by two again. So the number of “interestingly unique” decompositions is actually half the number of divisors.
The divisor function gives us the formula for how many divisors a number has: take the exponents of all the factors, add 1 to each exponent, and multiply them all together.
The search
Generating center values
The first step is to find values which could possibly work as E, the center cell. From Fermat’s theorem mentioned above, these are numbers with only 4k+1 factors.
To generate numbers with 4k+1 factors, I do a one-time creation of a
big list of the first 1,500,000,000 primes of the form 4k+1, which is
roughly up to 32 bits. This is saved in a file, which I then mmap
with the MAP_SHARED flag, which allows lots of copies of the program
to run at the same time, and all share the prime list in memory.
Then a depth-first search tries all combinations of primes from the list whose product is less than some upper bound, keeping track of all the factors and their exponents as it goes. Any product greater than a lower bound (which allows the search to be split into parallel sections) is checked in the next step.
Primes larger than the initial list are dealt with in a separate pass. We can only ever have one factor larger than the list (otherwise the result would be close to 64 bits, which is well beyond any reasonable upper limit for a search), so we generate large primes on the fly and launch the normal list-based depth-first search for each one after adding it to the factor list.
Almost there
Now we have a number x with only 4k+1 prime factors. We want try E=x as the center cell of configurations 7.VII and 7.VIII (the ones with a non-square in the center), and also try E=x2 as the center cell of configurations 7.I – 7.VI (the ones with a square in the center).
Since the magic sum is 3E, any two cells on opposite sides of the center must add to 2E. So we are looking for decompositions of 2x and 2x2 into squares.
Since the depth-first search keeps track of the factors and their exponents of the numbers it’s generating, it’s easy for it to also track the number of unique decompositions into squares for both x and x2 without doing a lot of extra math. The extra factor of 2 in there doesn’t change the number of decompositions, because all the extra divisors it creates are even – and Jacobi’s theorem shows us that those don’t have any effect because they are not congruent to either 1 or 3 mod 4.
We can do some quick initial pruning:
- All the configurations with a square in the center require at least two unique decompositions (there are at least two rows/diagonals where both ends must be a square). And since in this case we are decomposing 2x2, one of the decompositions will be just x2+x2, which doesn’t work since we require all cells of the magic square to be unique. So to have any hope of E=x2 working, we need at least three decompositions of 2x2.
- Both the configurations with a non-square in the center require at least 3 unique decompositions. Also, there is no point in checking this case if x is a square (all its factors are raised to even powers), because that will have been covered by the squared-center case.
This also helps a lot with the large-primes case. We need at least two factors to get two unique decompositions, which means we don’t have to generate every prime up to our search limit – only up to limit/5, because 5 is the smallest 4k+1 prime.
Checking a center value
I use the PARI code I borrowed from
WIMS
to compute the list of decompositions of the center cell into sums of
squares. Then we consider every pair of decompositions, placing them
into the magic square and then computing the four remaining cells and
checking whether they are squares. To check whether a number is a
square, I take the absolute value – the negative of a square is not
exactly what I’m looking for, but it’s still interesting – and do a
quick check of the low three bits, using the fact that all odd squares
are equal to 1 mod 8. After that I use GMP’s mpn_perfect_square_p
function.
In more detail:
Squared center case
We have two pairs of squares: a,b and c,d.
Each pair of squares sums to 2E, making it a magic line through the center. So each pair needs to be on opposite sides of the center square. There are three possibilities:
- both diagonals
- both center rows/columns
- one diagonal and one row
#1 and #2 are fully symmetric, so we only need to try one combination. #3 is not symmetric, and we need to try all four combinations created by swapping the elements of one pair and swapping the two pairs.
This gives us a total of 6 magic squares to consider, each with four new cells which we can compute from the 5 known cells. In the typical case where none of the new cells are squares, we need to test three cells per magic square to know that it can’t possibly contain 7 squares total. So the naive accounting is that there are 24 new cells, and we need to test at least 18 of them.
However only 16 of the new cells are unique, and we can make use of that to reduce the typical number of is_square checks to 11.
First we place the squares on the diagonals, because all four of the new cells will be useful again later:
a 3E-a-c c
3E-a-d E 3E-b-c
d 3E-b-d b
Next we do the four row/diagonal combinations, each of which will reuse two of the results from above:
3E-a-c a c | 3E-b-c c b
a+c-d E b+d-c | a+d-c E b+c-d
d b 3E-b-d | a d 3E-a-d
---------------------------+----------------------------
3E-d-b d b | 3E-a-d a d
b+d-a E a+c-b | a+d-c E b+c-d
a c 3E-a-c | c b 3E-b-c
Finally we do the two rows/columns. All four new cells here are distinct from the ones above so we can’t skip any checks to see if they are square, but we may be able to reuse some intermediate results in computing the cell values. We use the fact that the corner cells are half the sum of the opposite-side centers:
(b+d)/2 a (b+c)/2
c E d
(a+d)/2 b (a+c)/2
Non-squared center case
The check for E=x (non-squared center) is similar, but simpler because both configurations can be checked by placing the known squares symmetrically (on the diagonals or centers), so only two checks are needed. Here everything is done with 64-bit math, instead of 128-bit as with the squared-center case.
Avoiding common factors
If all four of the squares we are placing share a common factor with E, then we could just divide all the elements by their common factor and have an equivalent magic square with smaller numbers – which would already have been covered in our search. So we want to detect and avoid those cases. With a bit of algebra we can show that if we have A+B = 2E, then if A and E have a common factor, B must also be divisible by that same factor.
We already know the factors of E from the way it was constructed, so after computing all the possible decompositions of 2E into sums of squares, we can check one half of each decomposition to see whether it is divisible by E’s factors, and record the results in a bit vector of shared factors.
Then as we consider each pair of decompositions as described above, we can just AND their bit vectors together; if the result is non-zero, then both these decompositions share a common factor with E, and we should skip testing this pair.
An alternate method
This work was originally done around 2008, before Lee Morgenstern published a different method with an alternate way of generating two-square decompositions. Morgenstern’s method is the same in that it generates magic squares with 5 squared cells and then checks the other 4 to see if they are squares. But his search comes from the opposite direction – rather than choosing E and then computing the decompositions, it generates the decompositions directly and constructs E (and the other four squared cells).
This is clearly better in that it doesn’t waste time computing the decompositions into two squares, or doing the depth-first search to construct numbers with 4k+1 factors. The time in my search is heavily dominated by just checking all the squares which result from trying all pairs of decompositions, but still, it might be incrementally faster to upgrade to Morgenstern’s method. One aesthetic drawback is that because it generates 3-square progressions parametrically, it is hard to describe in simple terms what bounds have been searched.
Results
I threw a lot of CPU cycles at this, but unfortunately I have only disappointing results to report.
There are no more magic squares which use 7 or more squares which have a non-square central cell up to 1014, or a square central cell up to 1028.
The search considered over 3 trillion values for E, and checked about 875 trillion magic squares. It seems likely there is a solution out there… but whether it is within reach of any reasonable search I don’t know.